[BaekJoon] G5 2293 동전 1

Dynamic Programming . ..............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

'Java' 언어를 활용하여 본 알고리즘 문제를 해결하였습니다.

 

1. 문제

2293번: 동전 1

 

동전 1 문제

  

  

 

2. 이해

각 동전의 값들을 price 배열에 우선 넣었다.

 

일단 이 문제의 풀이를 위해 n=3, k=12,

각 동전의 값들은 1원, 2원, 4원이라고 해보자. 

 

처음 가장 기본적으로 생각해 본 것은, 경우의 수를 dp 배열에 담는 다고 하면, 아래와 같이 생각했다.

dp[j] = dp[j - price[0]] + dp[j - price[1]] + ... + dp[j - price[i-1]];

위 풀이의 뜻은 특정 동전의 합, j값을 조합하기 위한 경우의 수로

1원을 반드시 사용할 때 경우의 수 + 2원을 반드시 사용할 때 경우의 수 + 4원을 반드시 사용할 때 경우의 수

의 방식이라고 볼 수 있다.

 

그러나 위 방식은 문제에서 언급한 것을 무시하는 방식이다

사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.

 

만약 위 점화식을 사용한다면,  j=3일 때 (동전의 합을 활용해서 3원을 구성해야 한다.) 
dp[3] = dp[3 - 1] + dp[3 - 2] = 2 + 1 = 3이 된다. 

그러나 실제로 위 문제의 조건을 고려한다면, (1, 1) / (2) 의 총 2 가지 경우의 수가 나와야 정상이다.

 

따라서 위 점화식은 틀렸다.

 

---

 

두 번째 고려할 방식은 2차원 배열이다. 

>만약 문제의 조건 (n<=100)에 따라, n x n int형 2차원 배열을 만든다면, 10000 * 4KB = 거의 40MB에 육박하지만,

문제의 조건에 메모리 제한은 4MB임으로, 이 방식은 메모리 용량 초과를 만날 것이다.

 

---

 

그렇다면, 첫 번째 방식에서 위 순서를 고려한다는 조건을 어떻게 적용할 수 있을까?

 

첫 번째 방식은 각 j값 (동전의 합)의 경우의 수를 한 번에 확실하게 구하면서 다음 j값으로 넘어간다.  

그러나 이제 설명할 방식은 조금 다른데, 

 

각 동전의 합을 구할 때 사용하는 동전의 가지 수를 점차 늘려가며 이 값을 매번 배열에 추가해주는 방식이다. 

동전을 한 가지만 썼을 때의 경우의 수를 먼저 배열에 추가하고, 동전을 두 가지 썼을 때 경우의 수를 같은 배열에 추가하는 것의 방식을 동전의 개수만큼 반복한다.

  

 

1원 사용 시 dp 테이블

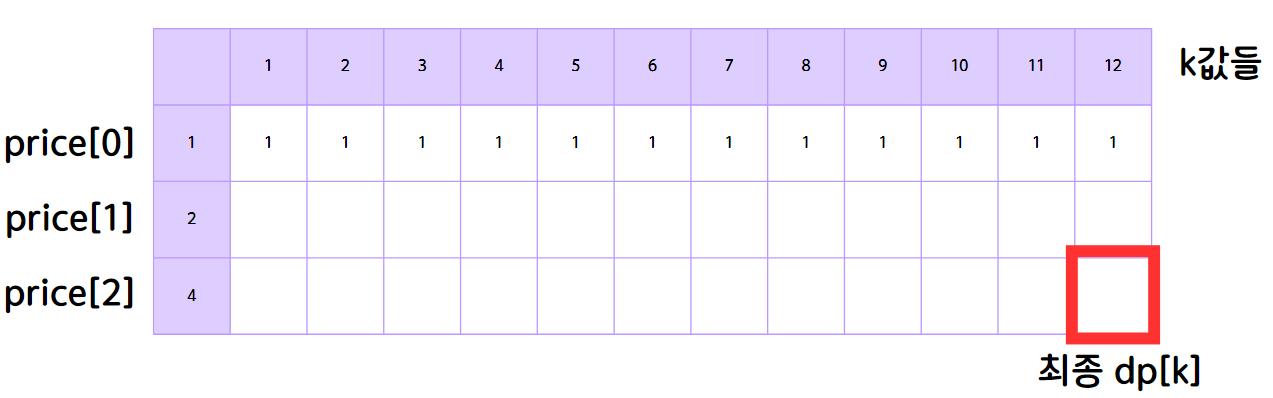
먼저 1원만 사용하여 동전의 합이 1원 ~ k원인 경우의 수는 위와 같다. 

어찌보면 당연하다.

 

2원 케이스 추가

그렇다면 price[1] row의 뜻은 뭘까? 

1원과 2원을 활용했을 때 해당 동전의 합(k)을 구할 수 있는 경우의 수다. 

 

그런데 녹색 네모 부분을 보자. 2원 동전으로 동전의 합 1을 만들 수 있을까? 

당연히 불가능하므로, price[1] 까지 고려했을 때 dp[1]은 price[0]만 고려했을 때의 dp[1] 값과 같다는 뜻이다. 즉, 1원으로만 동전의 합 1원을 조합할 수 있다는 말이다.

 

이 말은 곧,  k >= price[i] 일때만 dp 배열의 값에 경우의 수가 추가된다는 뜻이다. 

 

그리고, 만약 빨간 네모 아래 칸의 현재 dp[4]를 구한다고 생각해보자. (price[1] row)

1원과 2원을 활용해서 동전의 합 4를 만드는 조합을 구한다는 뜻이다.

 

price[1] row는 2원을 반드시 활용하는 동전의 합 4를 이루는 경우의 수를 기존 price[0] row (1원만 활용해서 동전의 합 4를 구한 경우의 수들)에 더하는 꼴이 된다.

 

즉, dp[4] = 기존 dp[4] + dp[4 - 2]의 형식이된다.

여기서 4는 k값들 중 하나일 것이고, 2는 price[1], 즉 이번 계산에서 반드시 포함한 2원이라는 뜻이다. 

위 식에서 dp[4 - 2]는, 구해야 하는 동전의 합 4원에서 반드시 필요한 2원을 제외한 2원을 price[0], price[1]로 구하는 경우의 수가 되는 것이다. 

 

이것을 점화식으로 나타내게 된다면 아래와 같다.

dp[0] = 1;

for (int value : price) {
    for (int j = value; j <= k; j++)
        dp[j] += dp[j - value];
}

  

  

3. 전체 코드

/*
* Memory : 11616 KB
* Time : 88ms
* */

package BaekJoon.Gold;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class G5_2293_동전_1 {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        st = new StringTokenizer(br.readLine(), " ");
        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        int[] price = new int[n];
        int[] dp = new int[k + 1];

        for(int i = 0; i< n; i++)
            price[i] = Integer.parseInt(br.readLine());

        dp[0] = 1;

        for (int value : price) {
            for (int j = value; j <= k; j++)
                dp[j] += dp[j - value];
        }

        System.out.println(dp[k]);
    }
}

 

4. 생각

dp 문제는 정말 풀어도 풀어도 어렵다.